Programs/R
[R_tidyverse] 분산분석 ANOVA: 이원분산분석 Two-way ANOVA
도마도다
2024. 2. 29. 15:45

분산분석 ANOVA
- 통계분석의 종류는 목적에 따라 크게 (그룹 간) 차이검정, (변수 간) 관계검정으로 나눌 수 있음. 이 중 그룹 간 차이를 검정하는 방법으로는 t-검정과 분산분석(ANOVA)이 있는데, t-검정은 그룹이 1~2개일 때 사용되며, ANOVA는 그룹이 3개 이상일 때 사용함.
- 분산분석은 이름에서 알 수 있듯이 데이터의 분산, 즉 데이터가 얼마나 퍼져있는지를 분석하는 방법임. 이를 통해 여러 그룹 간의 평균이 통계적으로 유의미하게 차이가 있는지를 판단함.
- 분산분석의 주요 가정은 정규성, 독립성, 등분산성임. 정규성은 각 그룹의 데이터가 정규분포를 따르는지, 독립성은 각 그룹의 데이터가 서로 독립적인지, 등분산성은 각 그룹의 데이터가 동일한 분산을 가지는지를 가정함.
- 분산분석의 종류
| 종류 | 특징 |
| 일원분산분석 One-way ANOVA |
1개의 독립변수가 있는 경우, 독립변수의 각 수준(그룹)간의 평균 차이를 검정 |
| 반복측정분산분석 Repeated Measures ANOVA |
1개의 독립변수와 반복 측정된 종속변수가 있는 경우, 독립변수의 각 수준(그룹)간의 평균 차이와 시간에 따른 변화를 검정 |
| 이원분산분석 Two-way ANOVA |
2개의 독립변수가 있는 경우, 독립변수들의 각 수준(그룹)간의 평균 차이를 검정하며, 또한 독립변수들 간의 상호작용 효과를 검정 |
| 이원반복측정분산분석 Two-way Repeated Measures ANOVA |
2개의 독립변수와 반복 측정된 종속변수가 있는 경우, 독립변수들의 각 수준(그룹)간의 평균 차이, 두 독립변수의 상호작용 효과, 그리고 시간에 따른 변화를 검정 |
이원분산분석 Two-way ANOVA 실습
*tidyverse 패키지를 활용한 분석방법
그룹을 구분하는 변수(요인)가 두 가지 일때 이원분산분석을 활용한다
두 가지 요인의 interaction effect를 보고 싶을 때 활용할 수 있다.
오늘의 실습에서는 치킨을 만들 때 온도(200도/ 300도)와 방법(오븐/ 기름)에 따른 맛의 점수의 차이를 살펴본다.
온도 그리고 방법이라는 두 가지 변수가 있기 때문에 이원분산분석을 활용한다.
주요 질문: 온도와 시간이 맛을 결정하는데 중요한 요인인지? 두가지 요인들 간 상호작용효과가 있는지?
귀무가설: 튀기는 온도와 방법 간에는 상호작용이 없다.
차례
<차례>
- 패키지 설치 및 불러오기
- 데이터 불러오기, 기술통계, 그래프그리기
- 이상치 제거
- 샤피로 테스트: 정규분포 검정
- 등분산검정
- 통계분석: ANOVA
- 사후검정: 다중비교
- 부록: 상호작용이 없을 경우
1. 패키지 설치 및 불러오기
오늘의 실습을 위해 필요한 R 패키지. 패키지는 한 번 설치하면 다음에 다시 설치할 필요 없음.
그러나 라이브러리는 매번 불러와야 함!
# 패키지 설치
install.packages("tidyverse") #쌍따옴표 주의
install.packages("tidymodels")
install.packages("rstatix")
install.packages("rskim")
#설치한 패키지 불러오기 (라이브러리)
library(tidyverse) #쌍따옴표 없음
library(tidymodels)
library(rstatix)
library(rskim)
2. 데이터 불러오기, 기술통계, 그래프 그리기
# 데이터 불러오기
twa_tb <- read_csv("10.twa.csv",
col_names = TRUE,
na = ".",
locale = locale("ko", encoding = "euc-kr")) %>%
mutate_if(is.character,as.factor) %>%
mutate(방법 = factor(방법,
levels = c(1,2),
labels = c("오븐", "기름"))) %>%
mutate(온도 = factor(온도,
levels = c(1,2),
labels = c("200도", "300도")))# 데이터의 구조 파악
str(twa_tb)
twa_tb
# 기술통계(그룹 쪼개기)
skim(twa_tb)
twa_tb %>%
group_by(방법, 온도) %>% # 방법, 온도 그룹쪼개서 확인(총 네개의 그룹)
get_summary_stats(맛점수)get_summary_stats(맛점수) 하면 아래와 같이 기초통계 확인 가능
# A tibble: 4 × 15
방법 온도 variable n min max median q1 q3 iqr mad mean sd se ci
<fct> <fct> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 오븐 200도 맛점수 14 84 91 87.5 86.2 89 2.75 2.22 87.5 2.03 0.542 1.17
2 오븐 300도 맛점수 16 91 98 94 92.8 95.2 2.5 2.22 94.2 2.04 0.51 1.09
3 기름 200도 맛점수 15 90 98 94 92.5 95.5 3 2.96 94 2.30 0.594 1.27
4 기름 300도 맛점수 15 84 88 86 85 87 2 1.48 86 1.20 0.309 0.662# 그래프 그리기
# 박스플랏, 히스토그램, 상호작용 그래프
twa_tb %>%
ggplot(mapping = aes(x = 방법,
y = 맛점수,
color = 방법)) + # 방법에 따라 색상을 다르게 해줘
geom_boxplot() +
facet_wrap(~온도) # 온도에 따라 그래프 따로 그려서 보여줘
twa_tb %>%
ggplot(mapping = aes(x = 맛점수)) +
geom_histogram(bins = 10,
color = "white",
fill = "steelblue",) +
facet_wrap(~ 방법*온도) 방법과 온도에 따라 그래프를 각각 그려서 보여줘
twa_tb %>%
group_by(온도, 방법) %>% # 온도에 따라 그룹핑 한 후에 방법에 따라 그룹핑한다
summarise(맛점수 = mean(맛점수)) %>% # 각 그룹의 맛점수 평균을 구하는 전처리 후, 그 값을 가지고 그래프를 그릴거야
ggplot(mapping = aes(x = 온도,
y = 맛점수,
color = 방법)) + # 방법에 따라 색깔 다르게
geom_line(mapping = aes(group = 방법)) + # 방법에 따라 나누어서 직선 그려줘
geom_point() # cross-over 됨, interaction effect가 있는 것으로 보임
# 200도에서는 기름일 때, 300도에서는 오븐일 때 맛점수가 좋게 나타남
# 다음 단계에서 이 상호작용 효과가 통계적으로도 나타나는가를 살펴볼 것임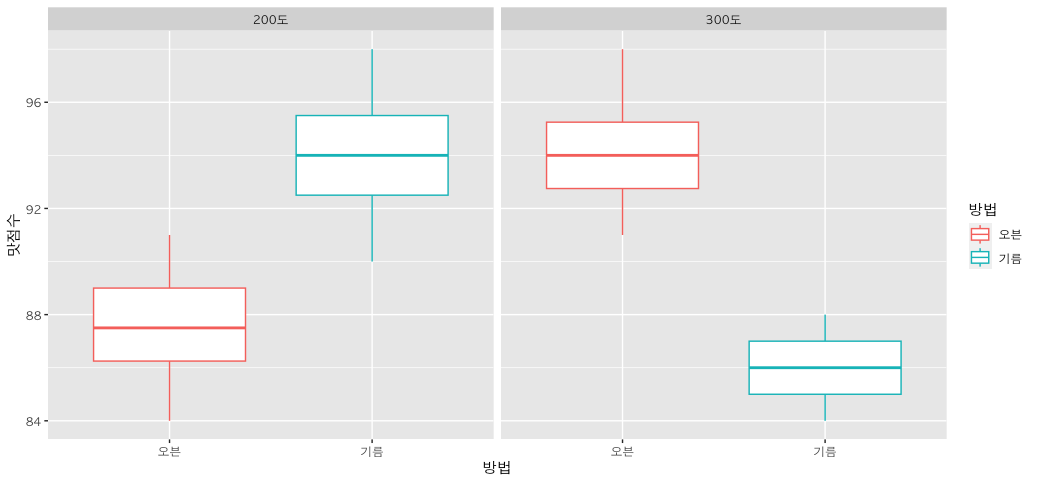


3. 이상치 제거
통계분석을 위해 분포에서 벗어나는 극단적인 값, 이상치를 제거해야 함. identify_outliers() 함수를 활용하면 간단히 파악 가능.
박스플랏에 나타나지 않았던 이상치가 나타나기도 함.
# 각각의 그룹을 나누어서 이상치 확인
twa_tb %>%
group_by(방법, 온도) %>%
identify_outliers(맛점수) 이상치 없음
[1] 방법 온도 맛점수 is.outlier is.extreme
<0 rows> (or 0-length row.names)
4. 샤피로 테스트: 정규분포검정
- 통계분석은 데이터의 분포가 정규분포일 것을 가정하고 이루어짐. 따라서 통계분석을 위해서는 이 데이터의 분포가 정규분포를 따르는지 검정해보아야 함.
- 그럴때 사용되는 것이 샤피로 테스트. 샤피로 테스트의 귀무가설은 '이 데이터의 분포가 정규분포를 따른다'는 것이고, 반대되는 대체가설은 '정규분포를 따르지 않는다' 가 됨. 샤피로 테스트의 p밸류 값이 0.05 이상이라면 귀무가설이 채택되면서 정규분포를 따른다고 볼 수 있음
- shapiro_test() 함수를 활용하면 됨
- 독립표본 t-검정에서는 각각의 그룹에 대해 확인해야 함
# 정규분포 검정
twa_tb %>%
group_by(방법, 온도) %>%
shapiro_test(맛점수) # 모두 정규분포위의 코드 입력 결과 아래와 같이 출력됨. 다 p밸류 0.05 이상이기 때문에 귀무가설이 채택됨. 즉, 이 데이터의 분포가 정규분포라고 받아들일 수 있음.
# A tibble: 4 × 5
방법 온도 variable statistic p
<fct> <fct> <chr> <dbl> <dbl>
1 오븐 200도 맛점수 0.970 0.876
2 오븐 300도 맛점수 0.961 0.683
3 기름 200도 맛점수 0.967 0.817
4 기름 300도 맛점수 0.918 0.181
5. 등분산검정
르벤테스트 실시, 귀무가설: 이 분포들은 등분산성을 가진다
twa_tb %>%
levene_test(맛점수 ~ 방법*온도)p밸류 0.05 이상 → 귀무가설 채택 → 등분산성 가진다
# A tibble: 1 × 4
df1 df2 statistic p
<int> <int> <dbl> <dbl>
1 3 56 1.46 0.235
6. 통계분석 : ANOVA
이제 시점 간 차이가 있다는 것은 알았는데 어느 시점 간에 차이가 있는지를 보고자 함. 아래의 코드 실행하여 ANOVA 테스트.
twa_results <- aov(맛점수 ~ 방법*온도,
data = twa_tb)
tidy(twa_results) # 상호작용 있음 -> 사후검정그 결과는 아래와 같음.
“방법:온도”는 상호작용을 보는 부분임. 귀무가설 기각 → 상호작용이 유의하게 나타났다~~
# A tibble: 4 × 6
term df sumsq meansq statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 방법 1 17.1 17.1 4.55 3.73e- 2
2 온도 1 6.77 6.77 1.81 1.84e- 1
3 방법:온도 1 807. 807. 215. 7.70e-21
4 Residuals 56 210. 3.75 NA NA
7. 사후검정: 다중비교
사후검정을 통해 구체적으로 그룹 간에 얼마나 차이가 있나 보자
twa_tb %>%
group_by(온도) %>% # 온도에 따른 방법의 차이가 있는가를 보겠다
pairwise_t_test(맛점수 ~ 방법,
p.adj = "bonferroni") # 기름은 200도에서 오븐은 300도에서 결과가 좋았다200도 오븐-기름, 300도 오븐-기름 둘 다 큰 차이가 있음
# A tibble: 2 × 10
온도 .y. group1 group2 n1 n2 p p.signif p.adj p.adj.signif
* <fct> <chr> <chr> <chr> <int> <int> <dbl> <chr> <dbl> <chr>
1 200도 맛점수 오븐 기름 14 15 1.20e- 8 **** 1.20e- 8 ****
2 300도 맛점수 오븐 기름 16 15 4.81e-14 **** 4.81e-14 ****
8. 부록: 상호작용이 없을 경우
twa_results <- aov(맛점수 ~ 방법 + 온도,
data = twa_tb)
tidy(twa_results)방법에 따라 맛점수 차이 없음, 온도에 따라 맛점수 차이없음
# A tibble: 3 × 6
term df sumsq meansq statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 방법 1 17.1 17.1 0.956 0.332
2 온도 1 6.77 6.77 0.379 0.540
3 Residuals 57 1017. 17.8 NA NA t-test 진행
twa_tb %>%
pairwise_t_test(맛점수 ~ 방법,
p.adj = "bonferroni") # 오븐- 기름 맛점수 차이 없음# A tibble: 1 × 9
.y. group1 group2 n1 n2 p p.signif p.adj p.adj.signif
* <chr> <chr> <chr> <int> <int> <dbl> <chr> <dbl> <chr>
1 맛점수 오븐 기름 30 30 0.33 ns 0.33 ns