[R_tidyverse] 분산분석 ANOVA: 일원분산분석 one-way ANOVA ②

 

 

 분산분석 ANOVA

• 통계분석의 종류는 목적에 따라 크게 (그룹 간) 차이검정, (변수 간) 관계검정으로 나눌 수 있음. 이 중 그룹 간 차이를 검정하는 방법으로는 t-검정과 분산분석(ANOVA)이 있는데, t-검정은 그룹이 1~2개일 때 사용되며, ANOVA는 그룹이 3개 이상일 때 사용함.
• 분산분석은 이름에서 알 수 있듯이 데이터의 분산, 즉 데이터가 얼마나 퍼져있는지를 분석하는 방법임. 이를 통해 여러 그룹 간의 평균이 통계적으로 유의미하게 차이가 있는지를 판단함.
• 분산분석의 주요 가정은 정규성, 독립성, 등분산성임. 정규성은 각 그룹의 데이터가 정규분포를 따르는지, 독립성은 각 그룹의 데이터가 서로 독립적인지, 등분산성은 각 그룹의 데이터가 동일한 분산을 가지는지를 가정함.

 

• 분산분석의 종류

일원분산분석  One-way ANOVA	1개의 독립변수가 있는 경우, 독립변수의 각 수준(그룹)간의 평균 차이를 검정
반복측정분산분석 Repeated Measures ANOVA	1개의 독립변수와 반복 측정된 종속변수가 있는 경우, 독립변수의 각 수준(그룹)간의 평균 차이와 시간에 따른 변화를 검정
이원분산분석  Two-way ANOVA	2개의 독립변수가 있는 경우, 독립변수들의 각 수준(그룹)간의 평균 차이를 검정하며, 또한 독립변수들 간의 상호작용 효과를 검정
이원반복측정분산분석 Two-way Repeated Measures ANOVA	2개의 독립변수와 반복 측정된 종속변수가 있는 경우, 독립변수들의 각 수준(그룹)간의 평균 차이, 두 독립변수의 상호작용 효과, 그리고 시간에 따른 변화를 검정

 

 

 

 

 

 

 

 

 

 

 

 

 추론 Infer 활용한 일원분산분석 one way ANOVA 실습

*tidyverse 패키지를 활용한 분석방법

• 추론 방식을 사용하여 ANOVA를 실시할 때는 부트스트래핑 방법을 활용할 수 있음
• 부트스트래핑: 데이터에서 여러 개의 샘플을 반복적으로 추출하여 새로운 분포를 만들어 내고, 이를 활용하여 통계적 추정이나 가설 검정을 수행하는 방법
• 사용되는 함수
• specify(): 어떤 데이터를 가져올거야?
• generate(): 데이터에서 가상의 샘플들을 뽑아줘 
• calculate(): 각각의 통계치 계산해
• visualize(): 새로운 분포 그래프 만들기
• hypothesize(): 귀무가설 가정

 

• 4개 집단(4개의 매장)의 고객만족도 점수에 유의한 차이가 있는지를 비교하기 때문에 One way ANOVA 실시

오늘 실습에서는 한 프랜차이즈 매장의 4개의 지점 간 고객만족도 점수의 차이가 있는지를 살펴본다
귀무가설: 4곳 매장의 고객만족도는 차이가 없다  

 

 

 

 

 

 차례

1. 패키지 설치 및 불러오기, 데이터 불러오기, 변수 설정
2. 추론을 활용한 가설검정: F값 검정

 

 

 

 

 

 

패키지 설치 및 불러오기, 데이터 불러오기, 변수설정

• 오늘의 실습을 위해 필요한 R 패키지. 패키지는 한 번 설치하면 다음에 다시 설치할 필요 없음. 그러나 라이브러리는 매번 불러와야 함!

# 패키지 설치
install.packages("tidyverse") #쌍따옴표 주의
install.packages("tidymodels")
install.packages("rstatix")

# 설치한 패키지 불러오기 (라이브러리)
library(tidyverse) #쌍따옴표 없음
library(tidymodels)
library(rstatix)

# 데이터 불러오기
owa_tb <- read_csv("08.owa.csv",
                   col_names = T,
                   na = ".",
                   locale = locale("ko", encoding = "euc-kr")) %>%
  mutate_if(is.character, as.factor) %>%
  mutate(매장명 = factor(매장명,
                         levels = c(1:4),
                         labels = c("강남","강서","강동","강북")))

 

 

 

 

 

 

 

 

 

추론을 활용한 가설검정: F값 검정

 

# F값확인
f_cal <- owa_tb %>%
  specify(formula = 만족도 ~ 매장명) %>%
  calculate(stat = "F") %>% 
  print() # 10.8

null_dist_f <- owa_tb %>%
  specify(formula = 만족도 ~ 매장명) %>%
  hypothesize(null = "independence") %>% # 그룹 간 차이이기 때문에 각각의 독립적인 값을 활용한다
  generate(reps = 1000,
           type = "permute") %>% # 퍼뮤트 방법 사용하겠다!
  calculate(stat = "F") %>%
  print()

 

위를 실행시키면 아래와 같이 출력됨. 1000번 추출한 샘플들 각각의 F값을 보여줌

 

Response: 만족도 (numeric)
Explanatory: 매장명 (factor)
Null Hypothesis: independence
# A tibble: 1,000 × 2
   replicate   stat
       <int>  <dbl>
 1         1 1.07  
 2         2 1.01  
 3         3 0.870 
 4         4 2.95  
 5         5 1.40  
 6         6 0.0897
 7         7 0.270 
 8         8 0.165 
 9         9 0.597 
10        10 0.763 
# ℹ 990 more rows
# ℹ Use `print(n = ...)` to see more rows
> 

 

 

신뢰구간 구하는 것은 의미가 없고, p밸류 구해서 그래프로 시각화함.

 

null_dist_f %>%
  get_p_value(obs_stat = f_cal,
              direction = "greater") # 큰지 작은지 비교하는 단측검정임

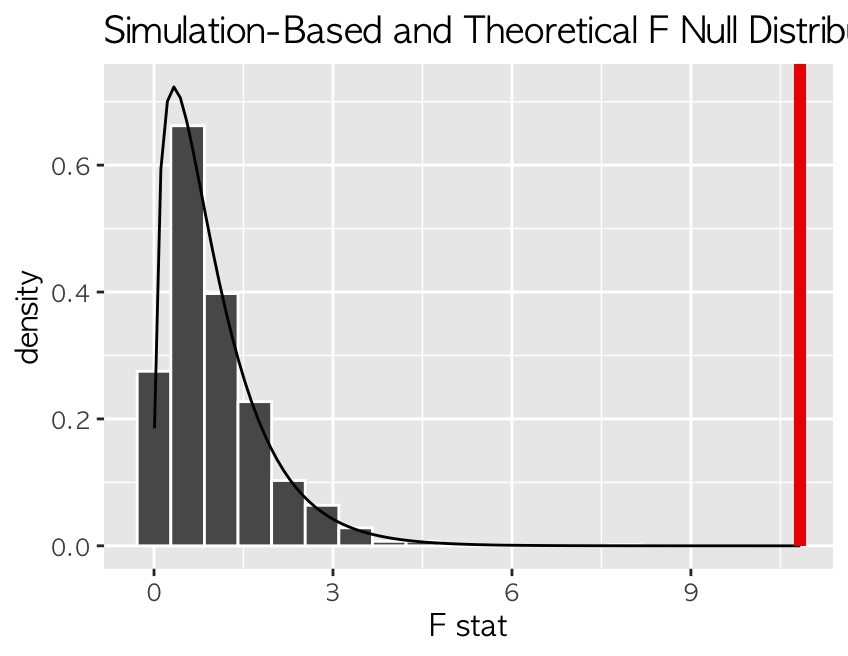
null_dist_f %>%
  visualize(method = "both") +
  shade_p_value(obs_stat = f_cal,
                direction = "greater") # 이론적 분포에서 많이 떨어져 있음 -> 귀무가설 기각